今回は、ブール代数と論理回路の基本を書き溜め、
新しく計算機科学を学ぶ人のためのマイルストーンを残していく。
ブール代数とは
まずブール代数についてWikipediaから引用する。
ブール代数（ブール束）とは束論における可補分配束（complemented distributive lattice）のことである。
(Wikipediaより)
ブール代数の深い内容については数学書に任せるとして、
大事なことは、ブール代数には４つの公理があり、
また、それによって現代のコンピューターが成り立っているという点である。
- 論理変数は0か1のどちらかの値をとる
- 0=1, 1=0
- A+0=0+A=A, A・1=1・A=A
- A+1=1+A=1, A・0=0・A=0
特にブール代数では下記の３つが基本的な演算方法であり、
コンピュータにおける２進数の世界では、
この3つを組み合わせることであらゆる計算が可能になる。
- AND
- OR
- NOT
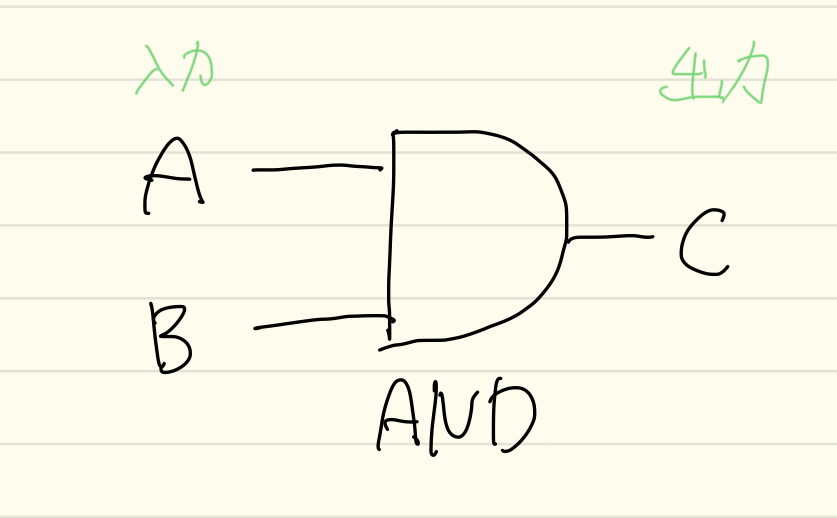
AND回路 論理積
ＡＮＤ回路では、入力が全て「１」のときのみ出力が「1」になります。
逆に、入力に「０」が一つでもあると出力は「０」になります。
論理回路記号は下記
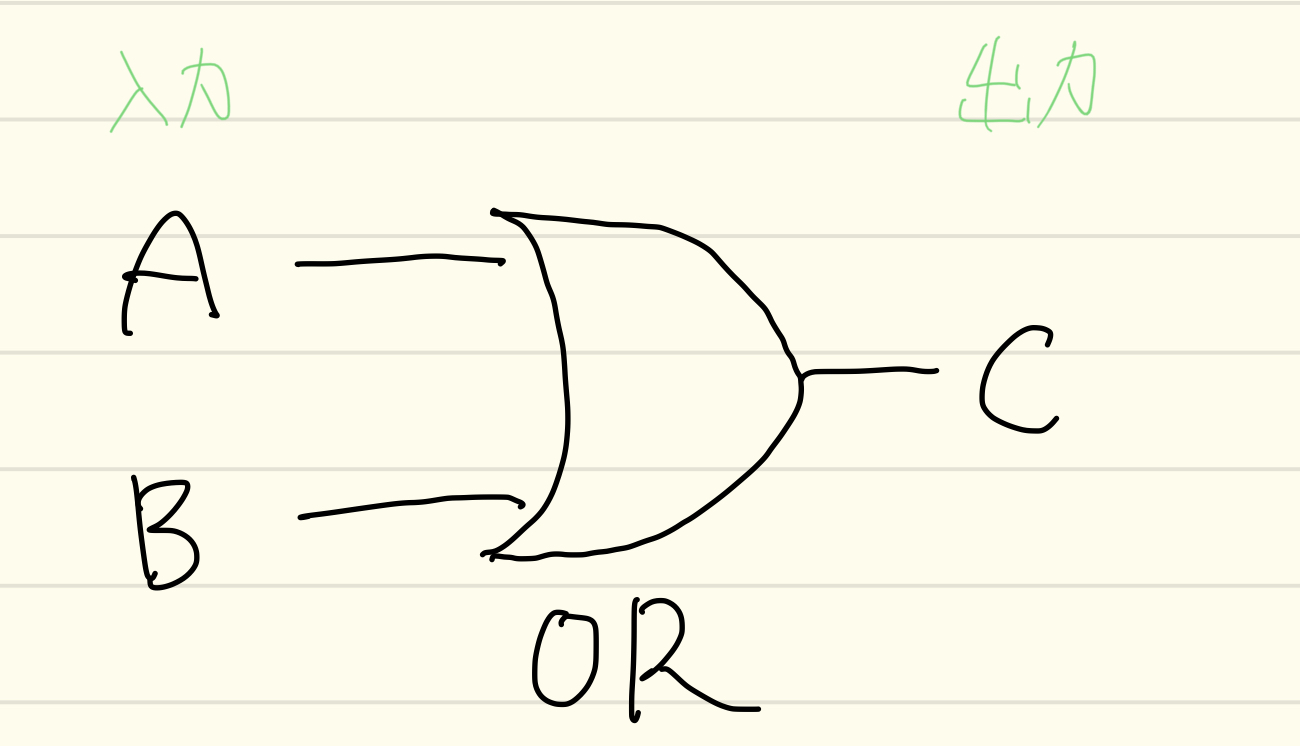
OR回路 論理和
ＯＲ回路では、入力のどれかが「１」であれば、出力は「１」になります。
逆に入力がすべて「０」のときのみ出力が「０」になります。
論理回路記号は下記
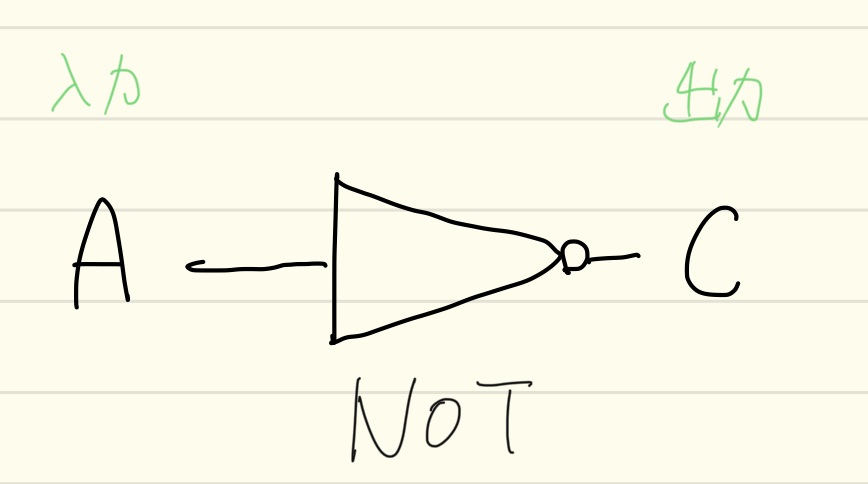
NOT回路 否定
ＮＯＴ回路は、入力に対して出力が反転されます。
「0」を入力すれば「1」になり、「1」を入力すれば「0」になります。
論理回路記号は下記
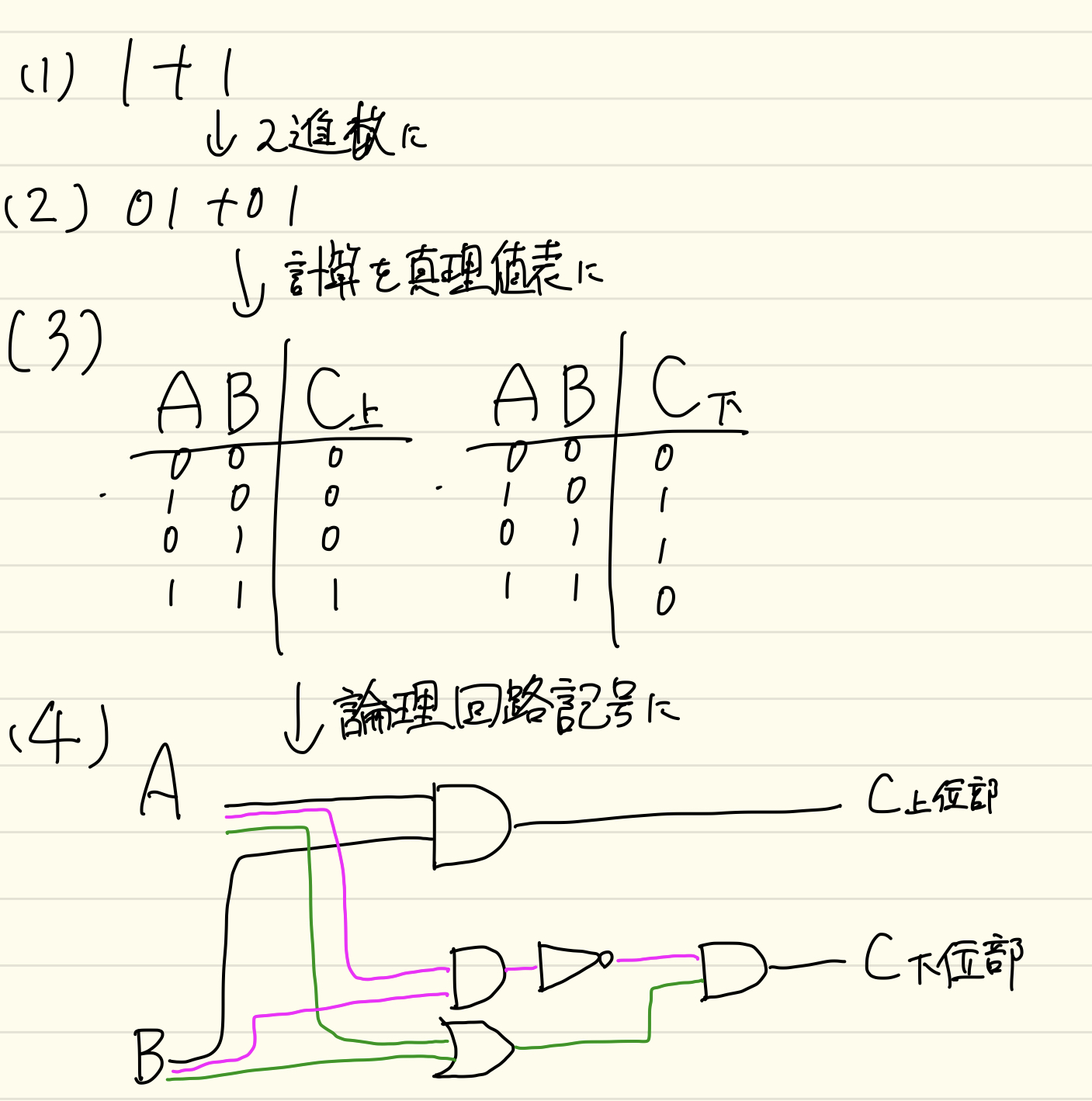
1+1の論理回路を描く
先の３つの論理回路記号を利用して
1+1の計算を行うと下記のような感じ。
ポイントは２つあり、
10進数は2進数に変換することと、bit上位部と下位部に分けて処理することである。
ブール代数と論理回路の基本記号を説明してください。
さて、先程の説明を読んだ人は、ブール代数と論理回路の基本記号を説明できますね。
確か３つありましたね？ どのような論理回路記号か描けますか？
ノートやメモに書くでも、Twitterに呟くでもYoutubeにアップロードするでも構いません。
今日知った情報をアウトプットしてみましょう。
正直文字列照合がうまく説明できていない気がする。
なので、詳しくは、参考をどうぞ。
じゃあね〜〜〜。